Recently a friend asked me a some questions:
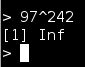
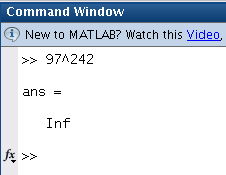
“97 raised to the power of 242 has equalled infinity on every calculator I’ve used, but it’s not infinite just very big. Why do they say infinity? And what is 97^242?”
The answer to the first part is easy; precision (and hence maximum values) are limited. Since this isn’t a basic intro to binary and computing we won’t go into it but just say in the good old days this would have resulted in the number simply wrapping. Modern devices and systems detect this overflow and show a special case result, usually Infinity/Inf or sometimes Not-a-Number/NaN.
Above are two common tools (R and Matlab) both running on 64-bit Linux and overflowing for 97^242. The difference in overflow can be seen in that the OSX Calculator can handle 97^71 but overflows at 96^72, whereas both Matlab and R will handle 97^166 but not 97^156.
Ok well Google has a calculator function so maybe we can just ask it for 97^242?
Alas, no. But maybe if we trick it with 97+242 to get it’s calculator up and then use that?
Nope. So how do we go about trying to calculate 97^242?
There are approaches we can use to estimate it (one of the most promising being looking for differences between powers of 100 and 97 then extrapolating, maybe something for another blog post) but we want an exact answer. As shown by Matlab/R and common logic built-in types are just too small and will overflow.
The solution comes, as with so much in life, from GNU in the GNU Multiple Precision Arithmetic Library aka GNU MP Bignum.
Once installed (yum install gmp-devel on Fedora) it’s just a case of hacking together some C to calculate the result (note the below isn’t supposed to be efficient, more transparent):
#include <gmp.h>
#include <stdio.h>
#include <stdlib.h>
int main(int ac, char** av)
{
mpz_t number,start;
unsigned long int startnumber = 97;
int i=0;
mpz_init(number);
mpz_init(start);
mpz_set_ui(start,startnumber);
mpz_set(number, start);
for (i=0; i<(242-1); ++i)
{
mpz_mul(number, number, start);
}
gmp_printf ("Answer: %Zd\n\n", number);
return 0;
}
Build this with: gcc bignum.c -lgmp -o bignum
And voila:
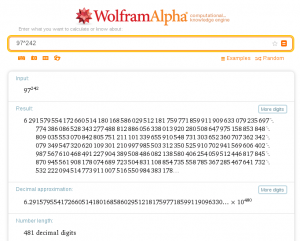
Answer: 6291579554172660514180168586029512181759771859911909633079235697774386086528343277488812886056338013920280508647975158853848809035553070842805751211101339655910548731303652360707362342079349547320620109301210997985503312350525910702941569606402987567610468491227904389508486082138580406254059512446817845870945561908178074689723504831108854735558785367285467641732532222094514773911007516550984383178257067496267923472962067697340265687768345831925754550553895144516227499602812609
Which for those who can’t be bothered to count digits is rounded as 6.29E+480.
Though of course after all this loading of libraries and writing of C it turns out that although Google couldn’t answer it, naturally Wolfram|Alpha could: